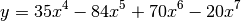5.5. Tools and classes¶
Contents
5.5.1. Classes¶
This module provides the Base class for PSDs
- class Spectrum(data, data_y=None, sampling=1.0, detrend=None, scale_by_freq=True, NFFT=None)¶
Base class for all Spectrum classes
All PSD classes should inherits from this class to store common attributes such as the input data or sampling frequency. An instance is created as follows:
>>> p = Spectrum(data, sampling=1024) >>> p.data >>> p.sampling
The input parameters are:
Parameters: - data (array) – input data (list or numpy.array)
- data_y (array) – input data required to perform cross-PSD only.
- sampling (float) – sampling frequency of the input data
- detrend (str) – detrend method ([None,’mean’]) to apply on the input data before computing the PSD. See detrend.
- scale_by_freq (bool) – divide the final PSD by
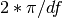
- NFFT (int) – total length of the final data sets (padded with zero if needed; default is 4096)
The input parameters are available as attributes. Additional attributes such as N (the data length), df (the frequency step are set (see constructor documentation for a complete list).
You can populate manually the psd attribute but you should respect the following convention:
- if the input data is real, the PSD is assumed to be one-sided (odd length)
- if the input data is complex, the PSD is assumed to be two-sided (even length).
When psd is set, sides is reset to its default value, NFFT and df are updated.
Spectrum instances have plotting utilities like plot() that take care of plotting the PSD versus the appropriate frequency range (based on sampling, NFFT and sides)
Note
the modification of some attributes (e.g., NFFT), makes the PSD obsolete. In such cases, the PSD must be re-computed before using plot() again.
At any time, you can get general information about the Spectrum instance:
>>> p = Spectrum(marple_data) >>> print p Spectrum summary Data length is 64 PSD not yet computed Sampling 1.0 freq resolution 0.015625 datatype is complex sides is twosided scal_by_freq is True
Constructor
Attributes:
From the input parameters, the following attributes are set:
The following read-only attributes are set during the initialisation:
And finally, additional read-write attributes are available:
- NFFT¶
Getter/Setter to the NFFT attribute.
Parameters: NFFT – a user choice for setting NFFT.
- if None, the NFFT is set to N, the data length.
- if ‘nextpow2’, computes the next power of 2 greater than or equal to the data length.
- if a integer is provided, it must be positive
- data¶
Getter/Setter for the input data. If input is a list, it is cast into a numpy.array. N, df and datatype are updated.
- data_y¶
Getter/Setter to the Y-data
- datatype¶
Getter to the datatype (‘real’ or ‘complex’). datatype is automatically updated when changing the data.
- detrend¶
Getter/Setter to detrend:
- None: do not perform any detrend.
- ‘mean’: remove the mean value of each segment from each segment of the data.
- ‘long-mean’: remove the mean value from the data before splitting it into segments.
- ‘linear’: remove linear trend from each segment.
- get_converted_psd(sides)¶
This function returns the PSD in the sides format
Parameters: sides (str) – the PSD format in [‘onesided’, ‘twosided’, ‘centerdc’] Returns: the expected PSD. from spectrum import * p = pcovar(marple_data, 15) p() centerdc_psd = p.get_converted_psd('centerdc')
- method¶
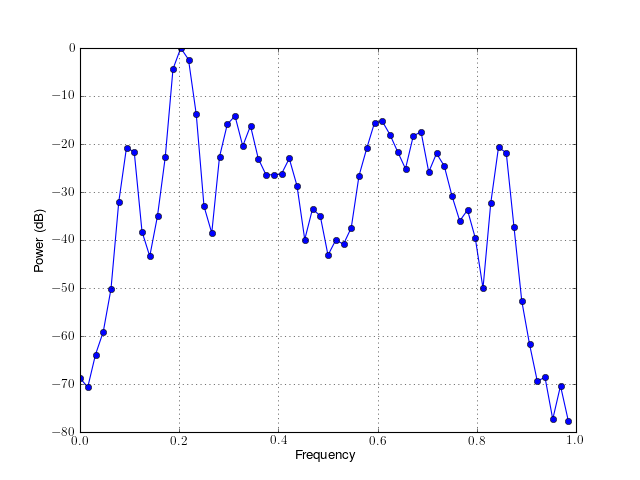
- plot(filename=None, norm=False, ylim=None, sides=None, **kargs)¶
a simple plotting routine to plot the PSD versus frequency.
Parameters: from spectrum import * p = Periodogram(marple_data) p() # runs the psd estimate p.plot(norm=True, marker='o')
- power()¶
Return the power contained in the PSD
if scale_by_freq is False, the power is:
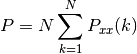
else, it is
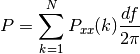
Todo
check these equations
- psd¶
Getter/Setter to psd
Parameters: psd (array) – the array must be in agreement with the onesided/twosided convention: if the data in real, the psd must be onesided. If the data is complex, the psd must be twosided. When you set this attribute, several attributes are set:
- range¶
Read only attribute to a Range object.
- run()¶
- scale()¶
- scale_by_freq¶
scale the PSD by
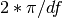
- class FourierSpectrum(data, sampling=1.0, window='hanning', NFFT=None, detrend=None, scale_by_freq=True, lag=-1)¶
Spectrum based on Fourier transform.
This class inherits attributes and methods from Spectrum. It is used by children class Periodogram, pcorrelogram and Welch PSD estimates.
The parameters are those used by Spectrum
Parameters: - data (array) – Input data (list or numpy.array)
- data_y – input data required to perform cross-PSD only.
- sampling (float) – sampling frequency of the input data
- detrend (str) – detrend method ([None,’mean’]) to apply on the input data before computing the PSD. See detrend.
- scale_by_freq (bool) – Divide the final PSD by
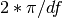
- NFFT (int) – total length of the data given to the FFT
In addition you need specific parameters such as:
Parameters: - window (str) – a tapering window. See Window.
- lag (int) – to be used by the pcorrelogram methods only.
This class has dedicated PSDs methods such as speriodogram(), which are equivalent to children class such as Periodogram.
from spectrum import datasets from spectrum import FourierSpectrum s = FourierSpectrum(datasets.data_cosine(), lag=32, sampling=1024, NFFT=512) s.periodogram() s.plot(label='periodogram') #s.correlogram() s.plot(label='correlogram') from pylab import legend, xlim legend() xlim(0,512)
Constructor
See the class documentation for the parameters.
Additional attributes to those inherited from
Spectrum are:
- lag¶
Getter/Setter used by the correlogram when autocorrelation estimates are required.
- periodogram()¶
An alias to Periodogram
The parameters are extracted from the attributes. Relevant attributes ares window, attr:sampling, attr:NFFT, attr:scale_by_freq, detrend.
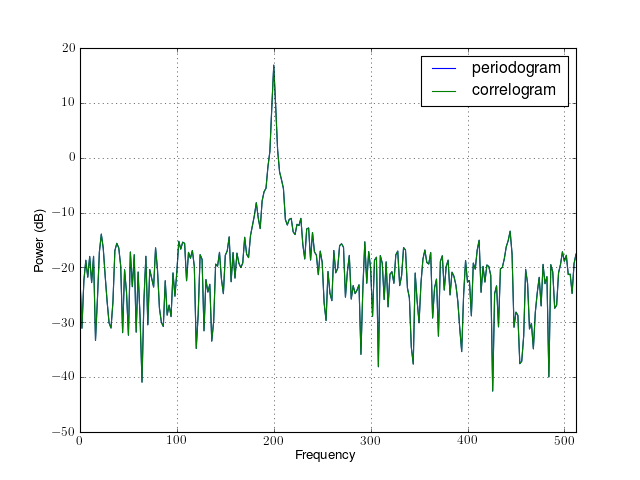
from spectrum import datasets from spectrum import FourierSpectrum s = FourierSpectrum(datasets.data_cosine(), sampling=1024, NFFT=512) s.periodogram() s.plot()
- window¶
Tapering window to be applied
- class ParametricSpectrum(data, sampling=1.0, ar_order=None, ma_order=None, lag=-1, NFFT=None, detrend=None, scale_by_freq=True)¶
Spectrum based on Fourier transform.
This class inherits attributes and methods from Spectrum. It is used by children class Periodogram, pcorrelogram and Welch PSD estimates. The parameters are those used by Spectrum.
Parameters: In addition you need specific parameters such as:
Parameters: - window (str) – a tapering window. See Window.
- lag (int) – to be used by the pcorrelogram methods only.
- NFFT (int) – Total length of the data given to the FFT
This class has dedicated PSDs methods such as periodogram(), which are equivalent to children class such as Periodogram.
[source code]from spectrum import datasets from spectrum import ParametricSpectrum data = datasets.data_cosine(N=1024) s = ParametricSpectrum(data, ar_order=4, ma_order=4, sampling=1024, NFFT=512, lag=10) #s.parma() #s.plot(sides='onesided') #s.plot(sides='twosided')
Exception occurred rendering plot.
Constructor
See the class documentation for the parameters.
Additional attributes to those inherited from Spectrum:
- ar¶
- ar_order¶
- ma¶
- ma_order¶
- plot_reflection()¶
- reflection¶
self.reflection = None elif method == ‘aryule’:
from spectrum import aryule ar, v, coeff = aryule(self.data, self.ar_order) self.ar = ar self.rho = v self.reflection = coeff
- rho¶
5.5.2. Correlation¶
Correlation module
Provides two correlation functions. CORRELATION() is slower than xcorr(). However, the output is as expected by some other functions. Ultimately, it should be replaced by xcorr().
For real data, the behaviour of the 2 functions is identical. However, for complex data, xcorr returns a 2-sides correlation.
| CORRELATION(x[, y, maxlags, norm]) | Correlation function |
| xcorr(x[, y, maxlags, norm]) | Cross-correlation using numpy.correlate |
- CORRELATION(x, y=None, maxlags=None, norm='unbiased')¶
Correlation function
This function should give the same results as xcorr() but it returns the positive lags only. Moreover the algorithm does not use FFT as compared to other algorithms.
Parameters: - x (array) – first data array of length N
- y (array) – second data array of length N. If not specified, computes the autocorrelation.
- maxlags (int) – compute cross correlation between [0:maxlags] when maxlags is not specified, the range of lags is [0:maxlags].
- norm (str) –
normalisation in [‘biased’, ‘unbiased’, None, ‘coeff’]
- biased correlation=raw/N,
- unbiased correlation=raw/(N-|lag|)
- coeff correlation=raw/(rms(x).rms(y))/N
- None correlation=raw
Returns: - a numpy.array correlation sequence, r[1,N]
- a float for the zero-lag correlation, r[0]
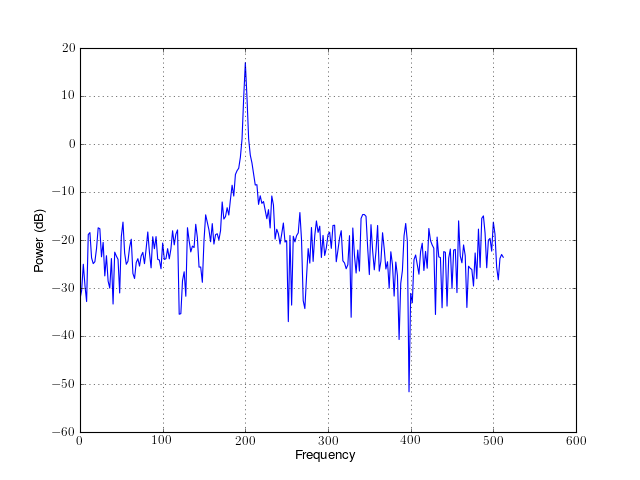
The unbiased correlation has the form:
![\hat{r}_{xx} = \frac{1}{N-m}T \sum_{n=0}^{N-m-1} x[n+m]x^*[n] T](../_images/math/c092e9187de013ec7f66487669b264defde8ed59.png)
The biased correlation differs by the front factor only:
![\check{r}_{xx} = \frac{1}{N}T \sum_{n=0}^{N-m-1} x[n+m]x^*[n] T](../_images/math/94918b30d8e8f0f1f364bf2111a2cb65922b3440.png)
with
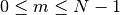 .
.>>> from spectrum import * >>> x = [1,2,3,4,5] >>> res = CORRELATION(x,x, maxlags=0, norm='biased') >>> res[0] 11.0
Note
this function should be replaced by xcorr().
See also
- xcorr(x, y=None, maxlags=None, norm='biased')¶
Cross-correlation using numpy.correlate
Estimates the cross-correlation (and autocorrelation) sequence of a random process of length N. By default, there is no normalisation and the output sequence of the cross-correlation has a length 2*N+1.
Parameters: - x (array) – first data array of length N
- y (array) – second data array of length N. If not specified, computes the autocorrelation.
- maxlags (int) – compute cross correlation between [-maxlags:maxlags] when maxlags is not specified, the range of lags is [-N+1:N-1].
- option (str) – normalisation in [‘biased’, ‘unbiased’, None, ‘coeff’]
The true cross-correlation sequence is
![r_{xy}[m] = E(x[n+m].y^*[n]) = E(x[n].y^*[n-m])](../_images/math/a367b3f2cd306e4c837f209664482a301493d678.png)
However, in practice, only a finite segment of one realization of the infinite-length random process is available.
The correlation is estimated using numpy.correlate(x,y,’full’). Normalisation is handled by this function using the following cases:
‘biased’: Biased estimate of the cross-correlation function
‘unbiased’: Unbiased estimate of the cross-correlation function
- ‘coeff’: Normalizes the sequence so the autocorrelations at zero
lag is 1.0.
Returns: - a numpy.array containing the cross-correlation sequence (length 2*N-1)
- lags vector
Note
If x and y are not the same length, the shorter vector is zero-padded to the length of the longer vector.
Examples
>>> from spectrum import * >>> x = [1,2,3,4,5] >>> c, l = xcorr(x,x, maxlags=0, norm='biased') >>> c array([ 11.])
See also
5.5.3. Tools¶
Tools module
| db2mag(xdb) | Convert decibels (dB) to magnitude |
| db2pow(xdb) | Convert decibels (dB) to power |
| mag2db(x) | Convert magnitude to decibels (dB) |
| nextpow2(x) | returns the smallest power of two that is greater than or equal to the |
| pow2db(x) | returns the corresponding decibel (dB) value for a power value x. |
| onesided_2_twosided(data) | Convert a two-sided PSD to a one-sided PSD |
| twosided_2_onesided(data) | Convert a one-sided PSD to a twosided PSD |
| centerdc_2_twosided(data) | Convert a center-dc PSD to a twosided PSD |
| twosided_2_centerdc(data) | Convert a two-sided PSD to a center-dc PSD |
Code author: Thomas Cokelaer, 2011
- centerdc_2_twosided(data)¶
Convert a center-dc PSD to a twosided PSD
- cshift(data, offset)¶
Circular shift to the right (within an array) by a given offset
Parameters: >>> from spectrum import cshift >>> cshift([0, 1, 2, 3, -2, -1], 2) array([-2, -1, 0, 1, 2, 3])
- fftshift(x)¶
wrapper to numpy.fft.fftshift
>>> from spectrum import fftshift >>> x = [100, 2, 3, 4, 5] >>> fftshift(x) array([ 4, 5, 100, 2, 3])
- mag2db(x)¶
Convert magnitude to decibels (dB)
The relationship between magnitude and decibels is:
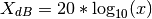
>>> mag2db(0.1) -20.0
See also
- nextpow2(x)¶
returns the smallest power of two that is greater than or equal to the absolute value of x.
This function is useful for optimizing FFT operations, which are most efficient when sequence length is an exact power of two.
Example : >>> x = [255, 256, 257] >>> nextpow2(x) array([8, 8, 9])
- onesided_2_twosided(data)¶
Convert a two-sided PSD to a one-sided PSD
In order to keep the power in the twosided PSD the same as in the onesided version, the twosided values are 2 times lower than the input data (except for the zero-lag and N-lag values).
>>> twosided_2_onesided([10, 4, 6, 8]) array([ 10., 2., 3., 3., 2., 8.])
- pow2db(x)¶
returns the corresponding decibel (dB) value for a power value x.
The relationship between power and decibels is:
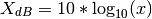
>>> x = pow2db(0.1) >>> x -10.0
- twosided(data)¶
return a twosided vector with non-duplication of the first element
>>> from spectrum import twosided >>> a = [1,2,3] >>> twosided(a) array([3, 2, 1, 2, 3])
- twosided_2_centerdc(data)¶
Convert a two-sided PSD to a center-dc PSD
- twosided_2_onesided(data)¶
Convert a one-sided PSD to a twosided PSD
In order to keep the power in the onesided PSD the same as in the twosided version, the onesided values are twice as much as in the input data (except for the zero-lag value).
>>> twosided_2_onesided([10, 2,3,3,2,8]) array([ 10., 4., 6., 8.])
5.5.4. datasets¶
The datasets module provides data sets to test the Spectrum functionalities.
| data_cosine([N, A, sampling, freq]) | Return a noisy cosine at a given frequency. |
| marple_data | list() -> new empty list |
| TimeSeries(data[, sampling]) | A simple Base Class for various data sets. |
Code author: Thomas Cokelaer 2011
| Reference: | [Marple] |
|---|
- class TimeSeries(data, sampling=1)¶
A simple Base Class for various data sets.
>>> data = [1, 2, 3, 4, 3, 2, 1, 0 ] >>> ts = TimeSeries(data, sampling=1) >>> ts.plot() >>> ts.dt 1.0
Parameters: - data (array) – input data (list or numpy.array)
- sampling – the sampling frequency of the data (default 1Hz)
- plot(**kargs)¶
Plot the data set, using the sampling information to set the x-axis correctly.
- data_cosine(N=1024, A=0.1, sampling=1024.0, freq=200)¶
Return a noisy cosine at a given frequency.
Parameters: ![x[t] = cos(2\pi t * f_0) + A w[t]](../_images/math/3b371c3687128ece7bfa53d723a66db102830feb.png)
where w[t] is a white noise of variance 1.
>>> a = data_cosine(N=1024, sampling=1024, A=0.5, freq=100)
- marple_data = [(1.349839091+2.011167288j), (-2.117270231+0.817693591j), (-1.786421657-1.291698933j), (1.162236333-1.482598066j), (1.641072035+0.372950256j), (0.072213709+1.828492761j), (-1.564284801+0.824533045j), (-1.080565453-1.869776845j), (0.92712909-1.743406534j), (1.891979456+0.972347319j), (-0.105391249+1.602209687j), (-1.618367076+0.63751328j), (-0.945704579-1.079569221j), (1.135566235-1.692269921j), (1.855816245+0.986030221j), (-1.032083511+1.414613724j), (-1.571600199+0.089229003j), (-0.243143231-1.444692016j), (0.838980973-0.985756695j), (1.516003132+0.928058863j), (0.257979959+1.170676708j), (-2.057927608+0.343388647j), (-0.578682184-1.441192508j), (1.584011555-1.011150956j), (0.614114344+1.508176208j), (-0.710567117+1.130144477j), (-1.100205779-0.584209621j), (0.150702029-1.217450142j), (0.748856127-0.804411888j), (0.795235813+1.114466429j), (-0.071512341+1.017092347j), (-1.732939839-0.283070654j), (0.404945314-0.78170836j), (1.293794155-0.352723092j), (-0.119905084+0.905150294j), (-0.522588372+0.437393665j), (-0.974838495-0.670074046j), (0.275279552-0.509659231j), (0.854210198-0.008278057j), (0.289598197+0.50623399j), (-0.283553183+0.250371397j), (-0.359602571-0.135261074j), (0.102775671-0.466086507j), (-0.00972265+0.030377999j), (0.185930878+0.8088696j), (-0.243692726-0.200126961j), (-0.270986766-0.460243553j), (0.399368525+0.249096692j), (-0.250714004-0.36299023j), (0.419116348-0.389185309j), (-0.050458215+0.702862442j), (-0.395043731+0.140808776j), (0.746575892-0.126762003j), (-0.55907619+0.523169816j), (-0.34438926-0.913451135j), (0.733228028-0.006237417j), (-0.480273813+0.509469569j), (0.033316225+0.087501869j), (-0.32122913-0.254548967j), (-0.063007891-0.499800682j), (1.239739418-0.013479125j), (0.083303742+0.673984587j), (-0.762731433+0.40897125j), (-0.895898521-0.364855707j)]¶
64-complex data length from Marple reference [Marple]
5.5.5. Linear Algebra Tools¶
5.5.5.1. cholesky¶
Cholesky methods
| CHOLESKY(A, B[, method]) | Solve linear system AX=B using CHOLESKY method. |
Code author: Thomas Cokelaer, 2011
- CHOLESKY(A, B, method='scipy')¶
Solve linear system AX=B using CHOLESKY method.
Parameters: - A – an input Hermitian matrix
- B – an array
- method (str) –
a choice of method in [numpy, scipy, numpy_solver]
- numpy_solver relies entirely on numpy.solver (no cholesky decomposition)
- numpy relies on the numpy.linalg.cholesky for the decomposition and numpy.linalg.solve for the inversion.
- scipy uses scipy.linalg.cholesky for the decomposition and scipy.linalg.cho_solve for the inversion.
Description
When a matrix is square and Hermitian (symmetric with lower part being the complex conjugate of the upper one), then the usual triangular factorization takes on the special form:
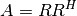
where
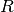 is a lower triangular matrix with nonzero real principal
diagonal element. The input matrix can be made of complex data. Then, the
inversion to find
is a lower triangular matrix with nonzero real principal
diagonal element. The input matrix can be made of complex data. Then, the
inversion to find 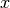 is made as follows:
is made as follows: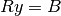
and
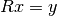
>>> import numpy >>> from spectrum import CHOLESKY >>> A = numpy.array([[ 2.0+0.j , 0.5-0.5j, -0.2+0.1j], ... [ 0.5+0.5j, 1.0+0.j , 0.3-0.2j], ... [-0.2-0.1j, 0.3+0.2j, 0.5+0.j ]]) >>> B = numpy.array([ 1.0+3.j , 2.0-1.j , 0.5+0.8j]) >>> CHOLESKY(A, B) array([ 0.95945946+5.25675676j, 4.41891892-7.04054054j, -5.13513514+6.35135135j])
5.5.5.2. eigen¶
- MINEIGVAL(T0, T, TOL)¶
Finds the minimum eigenvalue of a Hermitian Toeplitz matrix
The classical power method is used together with a fast Toeplitz equation solution routine. The eigenvector is normalized to unit length.
Parameters: - T0 – Scalar corresponding to real matrix element t(0)
- T – Array of M complex matrix elements t(1),...,t(M) C from the left column of the Toeplitz matrix
- TOL – Real scalar tolerance; routine exits when [ EVAL(k) - EVAL(k-1) ]/EVAL(k-1) < TOL , where the index k denotes the iteration number.
Returns: - EVAL - Real scalar denoting the minimum eigenvalue of matrix
- EVEC - Array of M complex eigenvector elements associated
Note
External array T must be dimensioned >= M
array EVEC must be >= M+1
Internal array E must be dimensioned >= M+1 .
- dependencies
5.5.5.3. levinson¶
Levinson module
| LEVINSON(r[, order, allow_singularity]) | Levinson-Durbin recursion. |
Code author: Thomas Cokelaer, 2011
- LEVINSON(r, order=None, allow_singularity=False)¶
Levinson-Durbin recursion.
Find the coefficients of a length(r)-1 order autoregressive linear process
Parameters: - r – autocorrelation sequence of length N + 1 (first element being the zero-lag autocorrelation)
- order – requested order of the autoregressive coefficients. default is N.
- allow_singularity – false by default. Other implementations may be True (e.g., octave)
Returns: - the N+1 autoregressive coefficients
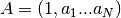
- the prediction errors
- the N reflections coefficients values
This algorithm solves the set of complex linear simultaneous equations using Levinson algorithm.
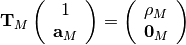
where
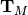 is a Hermitian Toeplitz matrix with elements
is a Hermitian Toeplitz matrix with elements
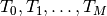 .
.Note
Solving this equations by Gaussian elimination would require
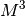 operations whereas the levinson algorithm
requires
operations whereas the levinson algorithm
requires 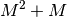 additions and
additions and 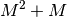 multiplications.
multiplications.This is equivalent to solve the following symmetric Toeplitz system of linear equations
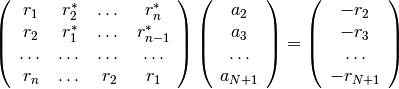
where
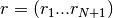 is the input autocorrelation vector, and
is the input autocorrelation vector, and
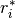 denotes the complex conjugate of
denotes the complex conjugate of 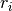 . The input r is typically
a vector of autocorrelation coefficients where lag 0 is the first
element
. The input r is typically
a vector of autocorrelation coefficients where lag 0 is the first
element 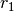 .
.>>> import numpy; from spectrum import LEVINSON >>> T = numpy.array([3., -2+0.5j, .7-1j]) >>> a, e, k = LEVINSON(T)
- levdown(anxt, enxt=None)¶
One step backward Levinson recursion
Parameters: - anxt –
- enxt –
Returns: - acur the P’th order prediction polynomial based on the P+1’th order prediction polynomial, anxt.
- ecur the the P’th order prediction error based on the P+1’th order prediction error, enxt.
- levup(acur, knxt, ecur=None)¶
LEVUP One step forward Levinson recursion
Parameters: - acur –
- knxt –
Returns: - anxt the P+1’th order prediction polynomial based on the P’th order prediction polynomial, acur, and the P+1’th order reflection coefficient, Knxt.
- enxt the P+1’th order prediction prediction error, based on the P’th order prediction error, ecur.
References : - Stoica R. Moses, Introduction to Spectral Analysis Prentice Hall, N.J., 1997, Chapter 3.
- rlevinson(a, efinal)¶
computes the autocorrelation coefficients, R based on the prediction polynomial A and the final prediction error Efinal, using the stepdown algorithm.
Works for real or complex data
Parameters: - a –
- efinal –
Returns: - R, the autocorrelation
- U prediction coefficient
- kr reflection coefficients
- e errors
A should be a minimum phase polynomial and A(1) is assumed to be unity.
Returns: - (P+1) by (P+1) upper triangular matrix, U,
- that holds the i’th order prediction polynomials
Ai, i=1:P, where P is the order of the input
polynomial, A.[ 1 a1(1)* a2(2)* ..... aP(P) * ] [ 0 1 a2(1)* ..... aP(P-1)* ]
- U = [ .................................]
- [ 0 0 0 ..... 1 ]
from which the i’th order prediction polynomial can be extracted using Ai=U(i+1:-1:1,i+1)’. The first row of U contains the conjugates of the reflection coefficients, and the K’s may be extracted using, K=conj(U(1,2:end)).
Todo
remove the conjugate when data is real data, clean up the code test and doc.
5.5.5.4. toeplitz¶
Toeplitz module
These functions are not yet used by other functions, which explains the lack of documentation, test, examples.
Nevertheless, they can be used for production.
| HERMTOEP(T0, T, Z) | solve Tx=Z by a variation of Levinson algorithm where T |
Code author: Thomas Cokelaer, 2011
- HERMTOEP(T0, T, Z)¶
solve Tx=Z by a variation of Levinson algorithm where T is a complex hermitian toeplitz matrix
Parameters: - T0 – zero lag value
- T – r1 to rN
Returns: X
used by eigen PSD method
5.5.5.5. linalg¶
Linear algebra tools
| csvd(A) | SVD decomposition using numpy.linalg.svd |
| corrmtx(x_input, m[, method]) | Correlation matrix |
| pascal(n) | Return Pascal matrix |
Code author: Thomas Cokelaer 2011
- pascal(n)¶
Return Pascal matrix
Parameters: n (int) – size of the matrix >>> pascal(6) array([[ 1., 1., 1., 1., 1., 1.], [ 1., 2., 3., 4., 5., 6.], [ 1., 3., 6., 10., 15., 21.], [ 1., 4., 10., 20., 35., 56.], [ 1., 5., 15., 35., 70., 126.], [ 1., 6., 21., 56., 126., 252.]])
Todo
use the symmetric property to improve computational time if needed
- csvd(A)¶
SVD decomposition using numpy.linalg.svd
Parameters: A – a M by N matrix Returns: - U, a M by M matrix
- S the N eigen values
- V a N by N matrix
See numpy.linalg.svd() for a detailed documentation.
Should return the same as in [Marple] , CSVD routine.
U, S, V = numpy.linalg.svd(A) U, S, V = cvsd(A)
- corrmtx(x_input, m, method='autocorrelation')¶
Correlation matrix
This function is used by PSD estimator functions. It generates the correlation matrix from a correlation data set and a maximum lag.
Parameters: Depending on the choice of the method, the correlation matrix has different sizes, but the number of rows is always m+1.
Method can be :
- ‘autocorrelation’: (default) X is the (n+m)-by-(m+1) rectangular Toeplitz matrix derived using prewindowed and postwindowed data.
- ‘prewindowed’: X is the n-by-(m+1) rectangular Toeplitz matrix derived using prewindowed data only.
- ‘postwindowed’: X is the n-by-(m+1) rectangular Toeplitz matrix that derived using postwindowed data only.
- ‘covariance’: X is the (n-m)-by-(m+1) rectangular Toeplitz matrix derived using nonwindowed data.
- ‘modified’: X is the 2(n-m)-by-(m+1) modified rectangular Toeplitz matrix that generates an autocorrelation estimate for the length n data vector x, derived using forward and backward prediction error estimates.
Returns: - the autocorrelation matrix
- R, the (m+1)-by-(m+1) autocorrelation matrix estimate R= X'*X.
Algorithm details:
The autocorrelation matrix is a
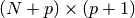 rectangular Toeplilz
data matrix:
rectangular Toeplilz
data matrix: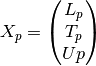
where the lower triangular
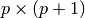 matrix
matrix 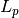 is
is![L_p =
\begin{pmatrix}
x[1] & \cdots & 0 & 0 \\
\vdots & \ddots & \vdots & \vdots \\
x[p] & \cdots & x[1] & 0
\end{pmatrix}](../_images/math/7165211c25d8ee405ff15363e1e9d663f9d84e72.png)
where the rectangular
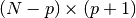 matrix
matrix 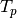 is
is![T_p =
\begin{pmatrix}
x[p+1] & \cdots & x[1] \\
\vdots & \ddots & \vdots \\
x[N-p] & \cdots & x[p+1] \\
\vdots & \ddots & \vdots \\
x[N] & \cdots & x[N-p]
\end{pmatrix}](../_images/math/54d0ed37147c4ee5f358efd7a4e9f66ebc40f607.png)
and where the upper triangular
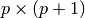 matrix
matrix 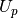 is
is![U_p =
\begin{pmatrix}
0 & x[N] & \cdots & x[N-p+1] \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & x[N]
\end{pmatrix}](../_images/math/bad67de33e9d4e3877661a1b579d18183f0239a5.png)
From this definition, the prewindowed matrix is
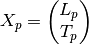
the postwindowed matrix is
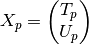
the covariance matrix is:
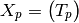
and the modified covariance matrix is:
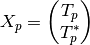
5.5.6. Waveforms¶
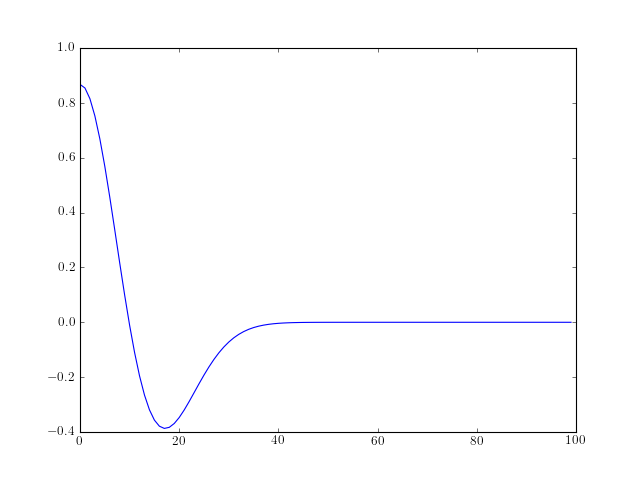
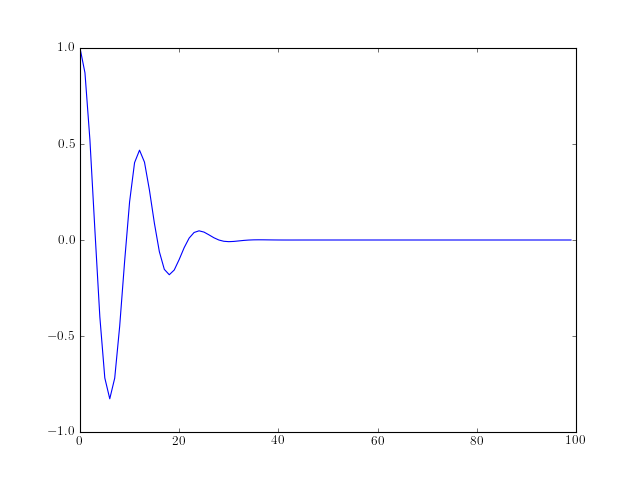
- morlet(lb, ub, n)¶
Generate the Morlet waveform
The Morlet waveform is defined as follows:
![w[x] = \cos{5x} \exp^{-x^2/2}](../_images/math/2ccfe596993d24bf2b2746289fa3f9df9f47d25e.png)
Parameters: - lb – lower bound
- ub – upper bound
- n (int) – waveform data samples
from spectrum import * from pylab import * plot(morlet(0,10,100))
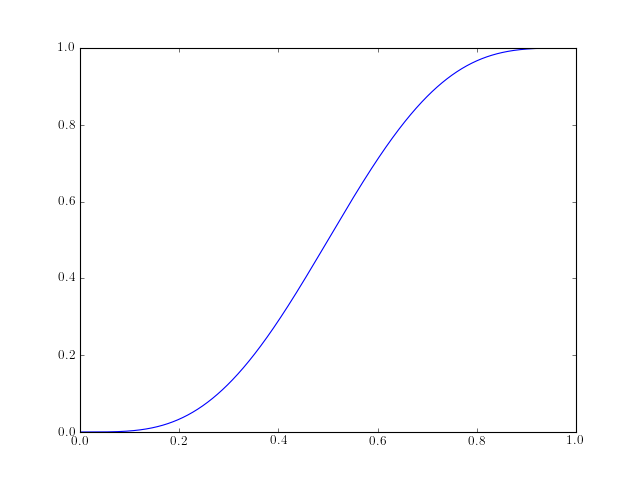
- chirp(t, f0=0.0, t1=1.0, f1=100.0, form='linear', phase=0)¶
Evaluate a chirp signal at time t.
A chirp signal is a frequency swept cosine wave.
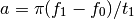
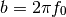
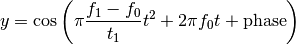
Parameters: The parameter form can be:
- ‘linear’
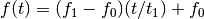
- ‘quadratic’
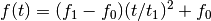
- ‘logarithmic’
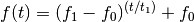
Example:
from spectrum import * from pylab import * t = linspace(0, 1, 1000) y = chirp(t, form='linear') plot(y) hold(True) y = chirp(t, form='quadratic') plot(y, 'r')
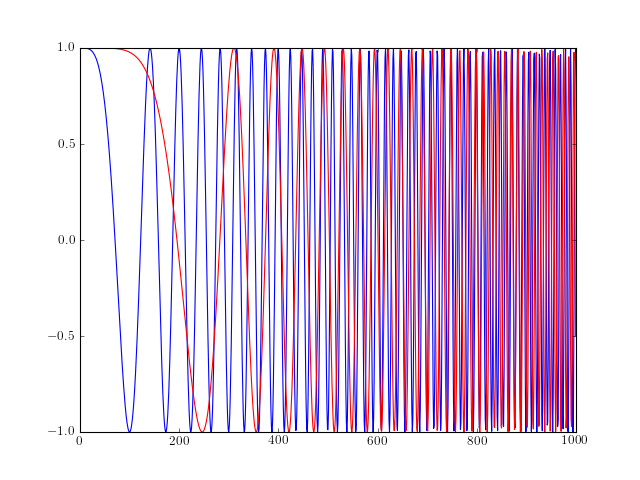
- ‘linear’
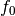 of the cosine.
of the cosine.